Planet 4 - Part 02 - Let's make some noise!

Introduction

To create earth-like planets, it is useful to start off with some continents.

When creating continents in simulation-oriented PCG, one customarily starts with a noise field and then apply simulated physical forces to make it more realistic.  In this article I will explain the workings and merits of a kind of noise function that I call "splat noise".

A Bit of History

A long, long time ago there were space games where planets were generated using a technique known as the fault-line technique.  Paul Bourke describes it here (scroll down to "Modelling fake planets"), but I will give a short summary in case that link goes dead some day.

The process is really simple: take a sphere, increase the altitude on a randomly chosen half and repeat as necessary.  The edges between the pairs of halves were referred to as fault-lines, hence the name of the technique.

Paul points out that this way always ends up with a perfectly anti-symmetric planet, and then he solves this by freeing the cutting plane from having to pass through the center of the sphere; each one now passes through a random point.  This unfortunately increases the number of iterations required to achieve the same level of detail.

He also demonstrates using it on a plane, and this is where I started when I invented splat noise.  My first problem with the planar fault-lines noise was that it did not wrap around at the edges.  Using a straight line that wraps around would be the obvious solution, but didn't work for various reasons that became apparent very quickly.  And the obvious solutions to these cause even further problems of similar difficulty.

The Invention of Splat Noise

So I decided to opt for a non-obvious solution instead.  I used circles instead of lines and it worked just as well.  Better even.  The fact that the effect of a circle is localized also opens up many new possibilities for further improvements.  One can vary the sizes of the circles, cluster them together, distribute them more evenly, optimize the processing, give the circles other profiles, use finite shapes other than circles...  The possibilities are endless and I often found the side-effects useful as well.

One of the things that I found surprising (at first) was that the horizontal profile of the splats affected the shapes visible vertically in the generated noise.  For instance, compare figures 1 and 2:

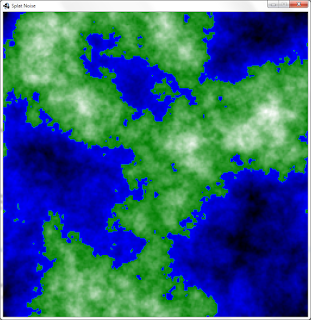Fig 1: Simple Cylinders

Fig 2: Steep Truncated Cones

These figures show that even a slight smoothing of the circle (or cylinder) gives a much smoother output.  I expect that convoluting the splat kernel is equivalent to convoluting the output.  Since the cylindrical kernel is mathematically simple, one can convolve it more precisely and much quicker than one can convolve the output noise.

A more surprising effect was that of varying the kernel size.  As seen in figure 3, below:

Fig 3: Randomly Sized Cylinders

One would expect that the uniform randomness of the distribution would nullify the effect of randomly varying the kernel size.  However, I have found that it does increase the variety of the sizes of the features generated.  In figure 3 one can see that it now forms both continents and islands.

 

In regard to figure 4: I used axis-aligned squares as the kernel.  Despite the individual squares being small, they combine into long straight lines crisscrossing the output.  Also, none of the original squares are discernible.

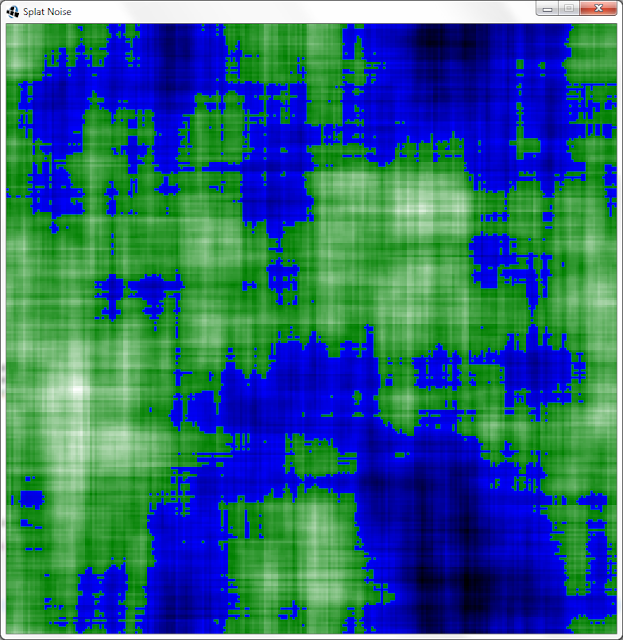Fig 4: Axially-Aligned Blocks

Further Observations

Other useful techniques that I have discovered include:

• Control the placement of continents by overlaying this noise over an existing map.
• The "existing map" mentioned above could be as simple as just random squiggles with a brush.
• Combine two splat noise outputs to create a distortion vector map to add detail to a smooth output field from some other algorithm without affecting the range of values.
• To calculate a section of an infinite world using only a finite number of kernels, divide the world into a grid, each with its own seed and providing only nearby kernel positions.

Conclusion

The Planet 4 project will certainly be using a spherical variant of splat noise to create its initial conditions, taking this algorithm full circle; back to its roots, but improved by the journey.

Random Number God - Introducing A.I. into P.C.G.

In all cases of Procedural Content Generation (P.C.G.) that I have come across, the use of random numbers is ubiquitous.  I believe that this lies at the core of the 'sameness' issue of P.C.G, and can be significantly mitigated by the use of artificial intelligence techniques.

Consider the difference between a sequence of random numbers and a sequence of numbers following a mathematical pattern.   This is the same as the difference between a random content generator and a smart one.

A common algorithm in A.I. is to create a tree of possible successive choices that it could make, and then choose the sequence of choices with the best outcome.  A brute force approach to this algorithm is generally extremely intensive in processing and memory, so the depth of the tree is usually artificially limited and heuristics are used to focus processing on the more promising choices.

However, for the purposes of P.C.G, the A.I. doesn't need to be particularly smart; even a weak A.I. can do better than just making random choices.  If one limits the A.I. to thinking one move ahead, one could easily upgrade an existing P.C.G. algorithm to include A.I. features.

To demonstrate, view this piece of pseudo-code:

feature = chooseRandomFeature();
applyFeature(feature);

The above will be found in many places in even the simplest P.C.G. algorithms.  Replace it with:

saveContent();

for each (feature in possibleFeatures)
{
    applyFeature(feature);
    value = evaluateContent();

    if (value > currentBestValue)
    {
        currentBestValue = value;
        currentBestFeature = feature;
    }

    revertContent();
}

applyFeature(currentBestFeature); 

This is of course still slower and using more memory than a random number generator, but will already give more pleasant results.  And this is only the beginning!

If one has the processing to spare, one could upgrade the above algorithm to think two moves ahead: generate two features before evaluating the content, and then apply only the first of these two.

In a P.C.G. algorithm that generates more than one kind of feature, there will be more than one of the above replacements, and hence, more than one A.I.  To improve the results even more, one could interleave the actions of the various A.I.s; making them take turns.  With judicious placement of the various evaluation functions and reversions one could even make the A.I.s predict what the others will do and then compete or cooperate as necessary.

If A.I. is adopted widely into P.C.G, I see a bright future for computer games.  Carmack's statement that P.C.G. is merely a very lossy compression algorithm will no longer be true.

Planet 4 - Part 01 - Making a Mesh

Introduction to this series is here.

Phase 1 is initiated.  I will adhere to a keep-it-simple approach during development.  So setting up the window went very quickly; no config files, no nothing.

The first step was to create the nodes in a spherical arrangement.  I divided the space into unit cubes and looped through them.  Where the innermost and outermost vertices of the cube was on opposite sides of the surface, I placed a node.

Each node represents a surface of about 128m×128m.  Since they're neither square nor uniform the area differs from node to node.  I experimented with different sized planets a bit and decided that radius 60 makes a medium-sized planet.  The circumference is about 48km, which is definitely much further than I have ever traveled in Minecraft.  What's the point of an infinite world, then?

Fig. 1: Radius 60 Sphere - Each node represents a 128m×128m area

Next I move the nodes so that they are no longer on the sphere, but rather arranged in a grid.  This will make noticing and understanding bugs much easier.

Fig. 2: Nodes are now aligned to a grid for debugging visualization

I reduce the size of the planet to radius 5, implement an algorithm for finding their nearest neighbours and link them up.  Ideally, I would have used Delaunay triangulation, but I decided to keep it simple instead; I have never done Delaunay triangulation before.  So I looped through the nodes and checked adjacent grid points for neighbours to link to.  The first time I only checked in the positive directions.  Figure 3 shows the inadequacy of this optimization:

Fig. 3: Added node-to-node links - My first bug is apparent

A simple fix is to just check the negative directions as well.  This does slow it down a bit though.  There is a faster way, but it is complicated, so I stuck to the simple way.

Fig. 4: Fixed the links bug

While my current algorithm does find every node that will contain a part of the sphere's surface, this causes some foreseeable problems, in that the double layer in some regions will stop the erosion algorithm from working correctly.  I take a cross section to see what it looks like (Fig.5) and see two possible solutions.  I could get rid of all diagonal links, or I could remove the extra layer before linking up the nodes.

Fig. 5: Cross section shows double layering

I decided to implement the node removal method, since this will simplify the eventual creation of the zones.  Each node that has three axis-aligned neighbours that are closer to the center is removed.  The cross section looks okay, so I switch back to the full sphere view:

Fig. 6: Removing the extra layer is not working as intended

That's no sphere!  I tried a few different techniques, with no positive results.  Eventually I realize the problem:  When I remove a node I change the circumstances of the surrounding nodes.  Near the axis-aligned planes that pass through the sphere's origin this causes that some nodes will no longer be removed.  The solution is to keep a set of nodes that need to be removed, and only remove them after all have been found.

Fig. 7: It works now

And finally I put the nodes back into their original spherical arrangement.

Fig. 8: Off the grid and back to a sphere